Task 3: How to Examine the Relationship Between Usual Intake of a Single Episodically-consumed Dietary Constituent and Some Outcome
In this example, the relationship between milk intake and osteoporosis treatment status (treatosteo) will be modeled. A participant was coded as having had treatment for osteoporosis if he or she responded “yes” to OSQ.070 (“{Were you/Was SP} treated for osteoporosis?”) from the osteoporosis questionnaire, and was set to “no” if he or she responded “no” to OSQ.070 or to OSQ.060 (“Has a doctor ever told {you/SP} that {you/s/he} had osteoporosis, sometimes called thin or brittle bones?”) from the osteoporosis questionnaire. (The SAS code to create this variable is found in the “Supplement Program” sample SAS code.)
This example uses the demoadv dataset (download at Sample Code and Datasets). The variables w0304_0 to w0304_16 are the weights (dietary weights and balanced repeated replication (BRR) weights) used in the analysis of 2003-2004 dietary data that requires the use of BRR to calculate standard errors. The model is run 17 times, including 16 runs using BRR (see Module 18, Task 4 for more information). BRR uses weights w0304_1 to w0304_16.
Note: If 4 years of NHANES data are used, 32 BRR runs are required. Additional weights are found in the demoadv dataset.
A SAS macro is a useful technique for rerunning a block of code when the analyst only wants to change a few variables; the macro BRR212 is created and called in this example. The BRR212 macro calls the MIXTRAN, DISTRIB, and INDIVINT macros, and calculates BRR standard errors of the parameter estimates. The MIXTRAN macro obtains preliminary estimates for the values of the parameters in the model, and then fits the model using PROC NLMIXED. It also produces summary reports of the model fit. Recall that modeling the complex survey structure of NHANES requires procedures that account for both differential weighting of individuals and the correlation among sample persons within a cluster. The SAS procedure NLMIXED can account for differential weighting by using the replicate statement. The use of BRR to calculate standard errors accounts for the correlation among sample persons in a cluster. Therefore, NLMIXED (or any SAS procedure that incorporates differential weighting) may be used with BRR to produce standard errors that are suitable for NHANES data without using specialized survey procedures. The DISTRIB macro estimates the distribution of usual intake, producing estimates of percentiles and the percent of the population below a cutpoint.
Note that the DISTRIB macro currently requires at least 2 cutpoints be requested in order to calculate the percent of the population below a cutpoint.
The MIXTRAN, DISTRIB, and INDIVINT macros used in this example were downloaded from the NCI website. Version 1.1 of the macros was used. Check this website for macro updates before starting any analysis. Additional details regarding the macro and additional examples also may be found on the website and in the users’ guide.
Step 1: Create one dataset so that each row corresponds to a single person day and define indicator variables if necessary, and create a second dataset for the INDIVINT macro
| Statements | Explanation |
|---|---|
data demoadv; |
First, select only those people with dietary data by selecting those without missing BRR weights. |
data adultf; |
Because the INDIVINT macro also requires a dataset with 1 record per person, a dataset called adultf for adult females ages 19 years and older is created. |
data day1;
data day2;
|
The variables d_milk_d1 and d_milk_d2 are calculated variables representing total milk consumed on days 1 and 2 respectively from all foods and beverages (see Module 4, Task 2 and Module 9, Task 4 for more details). To create a dataset with 2 records per person, the demoadv dataset is set 2 times to create 2 datasets, one where day=1 and one where day=2. The same variable name, d_milk, is used for calcium on both days. It is created by setting it equal to d_milk_d1 for day 1 and d_milk_d2 for day 2. |
| data milk; set day1 day2; run ; |
Finally, these data sets are appended. |
Step 2: Sort the dataset by respondent and day
It is important to sort the dataset by respondent and day of intake because the NLMIXED procedure uses this information to estimate the model parameters.
proc sort ; by seqn day; run ;
Step 3: Create the BRR212 macro
The BRR212 macro calls the MIXTRAN macro and computes standard errors of parameter estimates. After creating this macro and running it 1 time, it may be called several times, each time changing the macro variables.
| Statements | Explanation |
|---|---|
%include 'C:\NHANES\Macros\mixtran_macro_v1.1.sas' ; |
This code reads the MIXTRAN, DISTRIB, and INDIVINT macros into SAS so that these macros may be called. |
title2 "Task 3 - Milk and Osteoporosis Treatment" ; |
This title should be printed on all output. |
%macro BRR212(data, response, datam, var12, regresponse, foodtype, subject, repeat, covars_prob, covars_amt, outlib, modeltype, lambda, covars_reg, seq, weekend, vargroup, numvargroups, subgroup, start_val1, start_val2, start_val3, vcontrol, nloptions, titles, printlevel, cutpts, ncutpts, nsim_mc, byvar, t0, t1, final);
|
The start of the BRR212 macro is defined. All of the terms inside the parentheses are the macro variables. |
%MIXTRAN (data=&data, response=&response, foodtype=&foodtype, subject=&subject, repeat=&repeat, covars_prob=&covars_prob, covars_amt=&covars_amt, outlib=&outlib, modeltype=&modeltype, lambda=&lambda, replicate_var=w0304_0, seq=&seq, weekend=&weekend, vargroup=&vargroup, numvargroups= &numvargroups, subgroup=&subgroup, start_val1=&start_val1, start_val2=&start_val2, start_val3= &start_val3, vcontrol= &vcontrol, nloptions=&nloptions, titles= &titles, printlevel= &printlevel) |
Within the BRR212 macro, the MIXTRAN macro is called. All of the variables preceded by & will be defined by the BRR212 macro call. The only variable without an & is the replicate_var macro variable; it is set to w0304_0 for the first run. |
data parampred(keep = &subject a_var_u2 a_var_e a_lambda x2b2); |
Input datasets for the INDIVINT macro are created. The datasets _pred_unc_&foodtype and _param_unc_&foodtype are created in the MIXTRAN run. The syntax “if (_n_=1) then set” is a way of doing a 1-to-many merge, where the dataset _param_unc_&foodtype is merged with each row of the _pred_unc_&foodtype dataset. |
data parsubj1rec; merge parampred &datam(keep = &subject &var12); by &subject; run; |
The INDIVINT macro requires a dataset with only one line per person called parsubj1rec. This is defined by the macro variable datam in the BRR212 macro, and the response variables are defined by the macro variable var12. |
%DISTRIB (seed= 0 , nsim_mc= 100 ,modeltype=&modeltype, pred=& outlib.._ pred_&foodtype, param= & outlib.._ param_&foodtype, outlib=&outlib, subject=&subject,food=&foodtype); |
The DISTRIB macro is used to find the lambda for the transformation of the estimate of T (true usual intake) that will be used in the regression model. |
title&titles; title %eval (&titles+ 1 ); title "Task 3 - Milk and Osteoporosis Treatment" ;
|
This code clears the titles created in the DISTRIB macro and resets the title for the example. |
data _dist; set & outlib..d escript_&foodtype._w0304_0; keep tpercentile1-tpercentile99; run; |
The dataset descript_&foodtype_w0304_0 is from the DISTRIB macro. The percentiles are saved from this dataset. |
data _lambda (keep=lambda sse); do i= 1 to dim(z); MZ = mean(of Z1-Z99); MT = mean(of T1-T99); STZ = sum(of CP1-CP99); lambda = best_lambda; |
This code finds the best lambda to transform the estimate of T. This is done by finding the lambda that minimizes the error sum of squares. Z is the inverse of the normal cumulative distribution function (probit). At the end of the code, the best lambda is saved as a macro variable called lamt. |
proc univariate data=&data noprint; |
The minimum amount consumed on a consumption day is calculated and saved in a dataset called outmin_amt. |
data paramsubj1rec; proc sort; by &subject; run; |
The minimum amount is added to the dataset. Zero values are set to ½ of the mimimum amount. The dataset is sorted by subject. The variable lamt is created from the macro value lamt that was created previously. |
%indivint(model12= 2 , subj1recdata=paramsubj1rec, recid=&subject, r24vars=&var12, min_amt=min_amt, var_u1=p_var_u1, var_u2=a_var_u2, cov_u1u2=cov_u1u2, var_e=a_var_e, lambda=a_lambda, xbeta1=x1b1, xbeta2=x2b2, boxcox_t_lamt=y, lamt=lamt, dencalc=y, denopt=y, u1nlmix=, u2nlmix=, titles=&titles, notesprt=y); |
The INDIVINT macro is called. Because we are fitting a two-part model, the macro variable model12 is set equal to 2. This macro uses the dataset with 1 record per person (paramsubj1rec), and specifies the two 24-hour recall variables (var12). The minimum amount that was saved in the paramsubj1rec dataset is specified for the min_amt macro variable, as are the parameters that are saved in that dataset, including p_var_u1, a_var_u2, cov_u1u2, a_var_e, and a_lambda. The predicted values x1b1 and x2b2 from the MIXTRAN run are specified. The macro variable boxcox_t_lamt is set to y for ‘Yes’, indicating that a Box-Cox parameter is specified. This parameter is lamt, which was defined in the paramsubj1rec dataset in the last step. The macro variables dencalc, denopt, and notesprt are set to y for ‘Yes’, indicating that denominator integration is perfomed, denominator optimization is performed, and notes are printed in the SAS log, respectively. |
data subj1recres; |
The dataset _resdata is created in the INDIVINT macro. It is merged with the dataset adultf. |
proc reg data=subj1recres outest=regout; |
The regression model is run using the expected usual intake from the INDIVINT macro, called indusint. Because boxcox_t_lamt was set to y, this variable was already transformed in the INDIVINT macro, using the value of lamt in a Box-Cox transformation. Title3 is reset. |
data diethealthout0; |
The output dataset from the regression above (regout) is set, and the parameter for the expected true usual intake is renamed to rcbeta. In addition, lamt is saved, and the variables t0boxcox and t1boxcox and their difference multipled by rcbeta are computed. The macro variables t0 and t1 are set to a range that is relevant to the data, e.g., the 10th and 90th percentile. |
proc datasets nolist; delete parampred parsubj1rec paramsubj1rec subj1recres _resdata regout; run; |
Unneeded datasets are deleted. |
%do run= 1 %to 16 ; |
This code starts a loop to run the 16 BRR runs. |
%put ~~~~~~~~~~~~~~~~~~~ Run &run ~~~~~~~~~~~~~~~~~~~~; |
The run number is printed to the log. |
%MIXTRAN (data=&data, response=&response, foodtype= &foodtype, subject=&subject, repeat=&repeat, covars_prob=&covars_prob, covars_amt=&covars_amt, outlib=&outlib, modeltype=&modeltype, lambda=&lambda, replicate_var=w0304_&run, seq=&seq, weekend=&weekend, vargroup=&vargroup, numvargroups= &numvargroups, subgroup=&subgroup, start_val1=&start_val1, start_val2=&start_val2, start_val3=&start_val3, vcontrol=&vcontrol, nloptions=&nloptions, titles= &titles, printlevel=&printlevel) |
Within the BRR212 macro, the MIXTRAN macro is called. All of the variables preceded by & will be defined by the BRR212 macro call. The only variable without an & is the replicate_var macro variable; it is set to w0304_&run where &run equals 1 to 16. |
data parampred(keep = &subject a_var_u2 a_var_e a_lambda x2b2); if (_n_ = 1 ) then set & outlib.._ param_unc_&foodtype; set & outlib.._ pred_unc_&foodtype; run; |
Input datasets for the INDIVINT macro are created. The datasets _pred_unc_&foodtype and _param_unc_&foodtype are created in the MIXTRAN run. The syntax “if (_n_=1) then set” is a way of doing a 1-to-many merge, where the dataset _param_unc_&foodtype is merged with each row of the _pred_unc_&foodtype dataset. |
data parsubj1rec; merge parampred &datam(keep = &subject &var12); by &subject; run; |
The INDIVINT macro requires a dataset with only one line per person called parsubj1rec. This is defined by the macro variable datam in the BRR212 macro, and the response variables are defined by the macro variable var12. |
proc univariate data=&data noprint; |
The minimum amount consumed on a consumption day is calculated and saved in a dataset called outmin_amt. |
data paramsubj1rec; |
The minimum amount is added to the dataset. Zero values are set to ½ of the mimimum amount. The dataset is sorted by subject. The variable lamt is created from the macro value lamt that was created previously. |
%indivint(model12= 2 , subj1recdata=paramsubj1rec, recid=&subject, r24vars=&var12, min_amt=min_amt, var_u1=, var_u2=a_var_u2, cov_u1u2=, var_e=a_var_e, lambda=a_lambda, xbeta1=, xbeta2=x2b2, boxcox_t_lamt=y, lamt=lamt, dencalc=y, denopt=y, u1nlmix=, u2nlmix=, titles=&titles, notesprt=y); |
The INDIVINT macro is called. Because we are fitting a one-part model, the macro variable model12 is set equal to 2. This macro uses the dataset with 1 record per person (paramsubj1rec), and specifies the two 24-hour recall variables (var12). The minimum amount that was saved in the paramsubj1rec dataset is specified for the min_amt macro variable, as are the parameters that are saved in that dataset, including p_var_u1, a_var_u2, cov_u1u2, a_var_e, and a_lambda. The predicted values x1b1and x2b2 from the MIXTRAN run are specified. The macro variable boxcox_t_lamt is set to y for ‘Yes’, indicating that a Box-Cox parameter is specified. This parameter is lamt, which was defined in the paramsubj1rec dataset in the last step. The macro variables dencalc, denopt, and notesprt are set to y for ‘Yes’, indicating that denominator integration is perfomed, denominator optimization is performed, and notes are printed in the SAS log, respectively. |
data subj1recres; |
The dataset _resdata is created in the INDIVINT macro. It is merged with the dataset adultf. |
proc reg data=subj1recres outest=regout; |
The regression model is run using the expected usual intake from the INDIVINT macro, called indusint. Because boxcox_t_lamt was set to y, this variable was already transformed in the INDIVINT macro, using the value of lamt in a Box-Cox transformation. Title3 is reset. |
data diethealthout; |
The output dataset from the regression above (regout) is set, and the parameter for the expected true usual intake is renamed to rcbeta. In addition, lamt is saved, and the variables t0boxcox and t1boxcox and their difference multipled by rcbeta are computed. The macro variables t0 and t1 are set to a range that is relevant to the data, e.g., the 10th and 90th percentile. |
proc append base=brr_runs data=diethealthout; |
The BRR datasets are appended into a dataset called brr_runs. |
proc datasets nolist; delete parampred parsubj1rec paramsubj1rec subj1recres _resdata regout diethealthout; run; |
After appending the information to brr_runs, diethealthout and the other datasets created in the BRR runs can be deleted. |
%end ; |
The BRR runs end. |
data _null_; |
This code creates macro calls that are a list of the variables with the prefix ‘b’ and ‘db’. |
data parambrr; |
The brr_runs dataset is set, and a new dataset is created. This dataset renames the BRR parameters to have a prefix of ‘b’ using a rename statement and the macro calls created above. |
data ss; |
The estimates from the first run are merged with the BRR estimates, and the squared difference is computed for each BRR run. |
proc means data=ss sum; |
The sum of squares is computed. |
data brr; |
The standard errors are computed. |
data wparms; |
The point estimates are merged with the standard errors. |
proc transpose data=wparms out=wparmst; |
The data are transposed. |
data &final; |
The final dataset is created, and p-values and 95% confidence intervals are computed. |
proc print; |
The final dataset is printed. |
%mend BRR212; |
The end of the BRR212 macro is indicated. |
Step 4: Call the BRR212 macro
|
Note that SAS 9.2 TS1MO will produce an error with missing data in PROC IML, which is used in the INDIVINT macro. The problem is fixed in SAS 9.2 TS2M2. The SAS Problem Note documents the problem. From the HOT FIX tab a link to download the hot fix is available. This error is not encountered in SAS 9.1.3.
Step 5: Interpret output
- Depending on the printlevel selected, the output from each NLMIXED run will be printed in the output. The first NLMIXED output (replicate variable w0304_0) is a listing of the parameter estimates for the estimation of milk (see ‘Results from Fitting Correlated Model’). However, the standard errors are incorrect and are not printed in the summary table; BRR is needed to obtain estimates of the standard errors. The logistic regression model is also output for the base model. The other NLMIXED and LOGISTIC runs are from the BRR replications.
- The regression parameters and standard errors are printed at the end of the output.
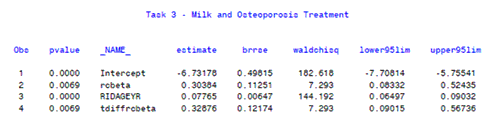
- The parameter rcbeta represents the relationship between usual intake of milk and treatement for osteoporosis, expressed in log odds of the Box Cox transformed estimate of usual intake for the individual.
- The relationship between usual milk intake and treatment for osteoporosis is significant (p=0.0069). The odds ratio for 1.5 cup equivalents of milk per day compared to 0.5 cup equivalents is 1.39 (95% CI 1.09,1.76).
Note: Your results may vary slightly, as a random seed is used to estimate the distribution of usual intake. However, they would not be expected to vary by more than 1%.